Associations, in several contexts called relations, are links between concepts, and even if they are labeled or not, explicit or implicit, they have assigned a meaning too. The split between concepts and labels introduces two perspectives:
1. Knowledge broken down to concepts in which some of the concepts function as associations between other concepts.
2. Represented knowledge broken down as labels in which some of the labels function as associations between other labels.
A simple example of association is the one implied by the object agent verb (OAV) construct, also called the object subject verb (OSV), that stands not only at the base of linguistics topology but also at the base of RDF triples (in this context referred as subject-predicate-object, concept-connection-concept or ‘entity-event-entity’) rooted in the linguistics topology. Such constructs are the “is-a” and “has-a” constructs, often used in knowledge representation. For example “whale is a sea mammal” could be expressed as (“whale”, “is-a”, “sea mammal”) and “whale has a tail” as (“whale”, “has-a’, “tail”) in (subject, predicate, object) notation, however representing knowledge as such triples is not an easy task, but the visual representation of such triples with nodes and links reduces the complexity to some degree.
The domain knowledge could be relatively expressed as such isolated triples, but in knowledge representation, in order to reduce the complexity of visualization and navigation, it’s simpler to join such triples when they have common concepts. Thus the two triples could be represented as follows:

The arrow shows in this case the agent, the first label in the sequence being the subject, while the label in between being the predicate. There are maps that don’t make use of arrows, in some cases the radial flow expressing the direction like in the case of Mind Maps, and maps in which there is no direction implied or a bidirectional row implies a bidirectional association, as in the case of synonymy.
The use of arrows and adequate labeling boxes facilitates KM’s understanding, in what concerns the role of labels in a triple, and navigation, in what concerns the flow/direction. As can be seen from the last diagram a subject could be involved in multiple associations, in the same way an object or predicate could be involved in multiple associations too. In the next KM could be observed for example how the same predicated is involved in multiple associations describing the anatomy of a whale.
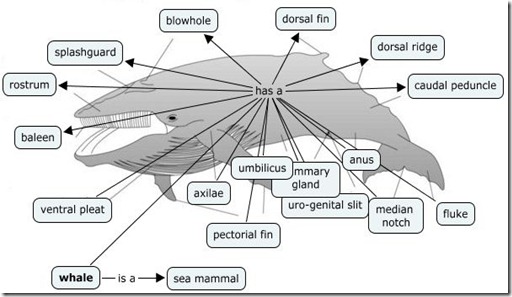
Whale Knowledge Map (adapted after whale anatomy)
The original representation could function as a K-map as well, though images are more difficult to process than the maps built with adequate software, the later offering also the possibility of conversion to a portable format that could be further processed. In addition the spatial disposition of concepts could play a role as well, in this case being correlated with the disposal within whale’s anatomy. In more complex KMs the use of “background” images is not always easy to embed, in addition the multitude of connections increasing the overall complexity. The form of representation could depend on each person’s preferences, the association could be explicit as well as implicit, and typically only one of them is use. Here are the same “has-a” associations represented with the help of circle map (implicit associations) and bubble map (explicit associations).
 |  |
| Bubble map | Circle Map |
The “is-a” and “has-a” associations are used in combination with any other types of associations, of importance being especially the causality (A causes B), synonymy (A is synonym of B) or antonymy (A is antonym of B), precedence (A precedes B) or concomitance (A occurs at the same time as B), etc. In fact any verb, substantive or even prepositions could play in theory the role of an association. If the above examples fall in the “verb as association” category, the use of substantives as associations is maybe more difficult to intuit, so here is an example based on whale’s anatomy in which the “has-a” has been replaced with “anatomic part” association:

Between two concepts there could be in theory multiple associations, more than one explicit association, though few are such cases because typically is stressed only the most important/relevant association. In the below image, a part of a KM on “self-transcending knowledge”, could be seen how the “competitive advantage” is involved in two associations with the same concept.
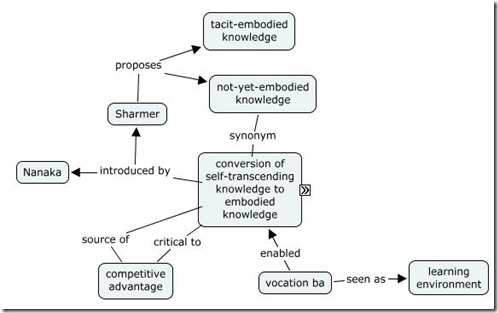
The existence of multiple associations has several other implications in what concerns associations’ type. For example causality implies two inverse associations: “A causes B”, respectively “B caused by A”, in fact dealing with the same meaning associated in different directions by inversion of terms. Such constructs could be confusing, therefore a good practice is to adopt only one of the two associations; the simplest approach is to simply use “A causes B”. A similar type of association is the transposed association, in which from “A imply B” is inferred that “Not-B imply Not-A”. With this we entered in the territory of deductive reasoning, entailment and of rules of inference.
Deductive reasoning could prove to be quite complex and of great use, especially when is intended to infer new associations (inferred associations) based on an existing set of associations. For example if in a KM we have that “A implies B” and “B implies A”, then we could deal with the equivalent association “A equivalent to B”, in mathematical terms expressed as “A=B”. Another simple logical inference is based on the simple rule of inference: if “A imply B” and “B imply C”, then “B imply C”. Implication could be applied also to causality, synonymy and several other types of associations.
The fact is that many of the rules of inference that apply is deductive reason could be used to KMs too, special inference engines could be used for this purpose. Associations between two or more concepts don’t have to be of the same type in order to prove to be useful, or in some cases even if the association seems to be of different types, the meaning they carry could be sufficient to allow an association to participate in inferences, this being valid especially for the associations belonging to the same class of meaning. In addition, associations of the same type and the concepts involved could reveal interesting properties that could be analyzed from the perspective of (superior) algebra or network theory.
Cardinality of Associations
The above representations have one important issue - they don’t reflect the cardinality of concepts, how many elements of the same concept participate in the associations. For example the whale has two blowholes and two pectorial fins, while a table has for legs, etc. In database modeling the associations, actually called relations, include the cardinality (e.g. 1-to-1, 1-to-n, n-to-n) though it just highlights that there is one or multiple records/entities associated in relations. In our case is typically required to specify the actual cardinality. As database model could be regarded as KM too, it’s thus necessary to address both types of cardinality, when they apply.
References:
[1] A. Kaiser, B. Fordinal. (2010). Creating a ba for generating self-transcending knowledge. Journal of Knowledge Management.Vol.14, no. 6 [Online] 10.1108/13673271011084943

No comments:
Post a Comment